Portal:Mathematics

• 
  Abacus, a ancient hand-operated calculating.
• 
  Portrait of Emmy Noether, around 1900.
• 
  Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Archimedes Thoughtful by Fetti (1620)

  
  Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
  
  Archimedes' other mathematical achievements include deriving an approximation of pi (π), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 

  

  
  Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
  
  Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
• 
  
  

  

  The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

  
  Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
  
  In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
• 
  
  

  

  Portrait by Jakob Emanuel Handmann, 1753

  
  Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ^ⓘ, Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
  
  Euler is credited for popularizing the Greek letter $\pi$ (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation $f(x)$ for the value of a function, the letter $i$ to express the imaginary unit ${\sqrt {-1}}$, the Greek letter $\Sigma$ (capital sigma) to express summations, the Greek letter $\Delta$ (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant $e$, the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
• 

  

  Plots of logarithm functions, with three commonly used bases. The special points log_b b = 1 are indicated by dotted lines, and all curves intersect in log_b 1 = 0.

  
  
  In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the 3rd power: 1000 = 10³ = 10 × 10 × 10. More generally, if x = b^y, then y is the logarithm of x to base b, written log_b x, so log₁₀ 1000 = 3. As a single-variable function, the logarithm to base b is the inverse of exponentiation with base b.
  
  The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written log x. (Full article...)
• 
  
  

  

  Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

  
  An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
  
  While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
  present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)

Good articles

• 

  

  The Shapley–Folkman lemma is illustrated by the Minkowski addition of four sets. The point (+) in the convex hull of the Minkowski sum of the four non-convex sets (right) is the sum of four points (+) from the (left-hand) sets—two points in two non-convex sets plus two points in the convex hulls of two sets. The convex hulls are shaded pink. The original sets each have exactly two points (shown as red dots).

  
  The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
  
  The lemma may be intuitively understood as saying that, if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex. (Full article...)
• 
  
  

  

  Portrait photograph of Alan Turing, taken on 29 March 1951.

  
  Alan Mathison Turing (/ˈtjʊərɪŋ/; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. Turing is widely considered to be the father of theoretical computer science.
  
  Born in London, Turing was raised in southern England. He graduated from King's College, Cambridge, and in 1938, earned a doctorate degree from Princeton University. During World War II, Turing worked for the Government Code and Cypher School at Bletchley Park, Britain's codebreaking centre that produced Ultra intelligence. He led Hut 8, the section responsible for German naval cryptanalysis. Turing devised techniques for speeding the breaking of German ciphers, including improvements to the pre-war Polish bomba method, an electromechanical machine that could find settings for the Enigma machine. He played a crucial role in cracking intercepted messages that enabled the Allies to defeat the Axis powers in many engagements, including the Battle of the Atlantic. (Full article...)
• 
  
  

  

  1963 statue of Anania Shirakatsi holding a globe at the entrance of the Matenadaran

  
  Anania Shirakatsi (Old Armenian: Անանիա Շիրակացի, Anania Širakac’i, anglicized: Ananias of Shirak) was a 7th-century Armenian polymath and natural philosopher, author of extant works covering mathematics, astronomy, geography, chronology, and other fields. Little is known for certain of his life outside of his own writings, but he is considered the father of the exact and natural sciences in Armenia—the first Armenian mathematician, astronomer, and cosmographer.
  
  A part of the Armenian Hellenizing School and one of the few secular scholars in medieval Armenia, Anania was educated primarily by Tychicus, in Trebizond. He composed science textbooks and the first known geographic work in classical Armenian (Ashkharhatsuyts), which provides detailed information about Greater Armenia, Persia and the Caucasus (Georgia and Caucasian Albania). (Full article...)
• 

  

  The logo of the International Mathematical Olympiad

  
  
  The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. It is widely regarded as the most prestigious mathematical competition in the world. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980. More than 100 countries participate. Each country sends a team of up to six students, plus one team leader, one deputy leader, and observers.
  
  Awards are given to approximately the top-scoring 50% of the individual contestants. Teams are not officially recognized—all scores are given only to individual contestants, but team scoring is unofficially compared more than individual scores. (Full article...)
• 

  

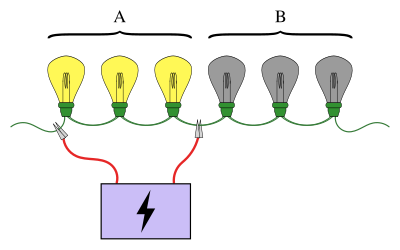
  An illustration of the lightbulb problem, where one is searching for a broken bulb among six lightbulbs. Here, the first three are connected to a power supply, and they light up (A). This indicates that the broken bulb must be one of the last three (B). If instead the bulbs did not light up, one could be sure that the broken bulb was among the first three. Continuing this procedure can locate the broken bulb in no more than three tests, compared to a maximum of six tests if the bulbs are checked individually.

  
  
  In statistics and combinatorial mathematics, group testing is any procedure that breaks up the task of identifying certain objects into tests on groups of items, rather than on individual ones. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that can be applied to a wide range of practical applications and is an active area of research today.
  
  A familiar example of group testing involves a string of light bulbs connected in series, where exactly one of the bulbs is known to be broken. The objective is to find the broken bulb using the smallest number of tests (where a test is when some of the bulbs are connected to a power supply). A simple approach is to test each bulb individually. However, when there are a large number of bulbs it would be much more efficient to pool the bulbs into groups. For example, by connecting the first half of the bulbs at once, it can be determined which half the broken bulb is in, ruling out half of the bulbs in just one test. (Full article...)
• 
  Ronald Paul "Ron" Fedkiw (born February 27, 1968) is a full professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and machine learning. His techniques have been employed in many motion pictures. He has earned recognition at the 80th Academy Awards and the 87th Academy Awards as well as from the National Academy of Sciences.
  
  His first Academy Award was awarded for developing techniques that enabled many technically sophisticated adaptations including the visual effects in 21st century movies in the Star Wars, Harry Potter, Terminator, and Pirates of the Caribbean franchises. Fedkiw has designed a platform that has been used to create many of the movie world's most advanced special effects since it was first used on the T-X character in Terminator 3: Rise of the Machines. His second Academy Award was awarded for computer graphics techniques for special effects for large scale destruction. Although he has won an Oscar for his work, he does not design the visual effects that use his technique. Instead, he has developed a system that other award-winning technicians and engineers have used to create visual effects for some of the world's most expensive and highest-grossing movies. (Full article...)
• 

  

  Selected witch of Agnesi curves (green), and the circles they are constructed from (blue), with radius parameters $a=1$, $a=2$, $a=4$, and $a=8$.

  
  
  In mathematics, the witch of Agnesi (Italian pronunciation: [aɲˈɲeːzi, -eːsi; -ɛːzi]) is a cubic plane curve defined from two diametrically opposite points of a circle.
  
  The curve was studied as early as 1653 by Pierre de Fermat, in 1703 by Guido Grandi, and by Isaac Newton. It gets its name from Italian mathematician Maria Gaetana Agnesi who published it in 1748. The Italian name la versiera di Agnesi is based on Latin versoria (sheet of sailing ships) and the sinus versus.
  This was read by John Colson as l’avversiera di Agnesi, where avversiera is translated as "woman who is against God" and interpreted as "witch". (Full article...)
• 

  

  A spiral staircase in the Cathedral of St. John the Divine. Several helical curves in the staircase project to hyperbolic spirals in its photograph.

  
  
  A hyperbolic spiral is a type of spiral with a pitch angle that increases with distance from its center, unlike the constant angles of logarithmic spirals or decreasing angles of Archimedean spirals. As this curve widens, it approaches an asymptotic line. It can be found in the view up a spiral staircase and the starting arrangement of certain footraces, and is used to model spiral galaxies and architectural volutes.
  
  As a plane curve, a hyperbolic spiral can be described in polar coordinates $(r,\varphi )$ by the equation
  $$r={\frac {a}{\varphi }},$$
  for an arbitrary choice of the scale factor $a.$ (Full article...)
• 

  

  The brute force algorithm finds a 4-clique in this 7-vertex graph (the complement of the 7-vertex path graph) by systematically checking all C(7,4) = 35 4-vertex subgraphs for completeness.

  
  
  In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size.
  
  The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...)
• 

  

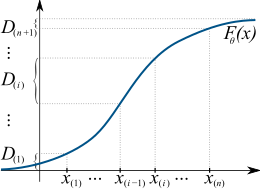
  The maximum spacing method tries to find a distribution function such that the spacings, D_(i), are all approximately of the same length. This is done by maximizing their geometric mean.

  
  
  In statistics, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model. The method requires maximization of the geometric mean of spacings in the data, which are the differences between the values of the cumulative distribution function at neighbouring data points.
  
  The concept underlying the method is based on the probability integral transform, in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity. (Full article...)
• 

  

  YBC 7289

  
  YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest known computational accuracy ... in the ancient world". The tablet is believed to be the work of a student in southern Mesopotamia from some time between 1800 and 1600 BC. (Full article...)
• 

  

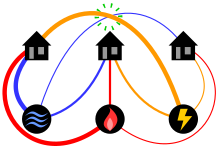
  Diagram of the three utilities problem showing lines in a plane. Can each house be connected to each utility, with no connection lines crossing?

  
  The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.
  
  This puzzle can be formalized as a problem in topological graph theory by asking whether the complete bipartite graph $K_{3,3}$, with vertices representing the houses and utilities and edges representing their connections, has a graph embedding in the plane. The impossibility of the puzzle corresponds to the fact that $K_{3,3}$ is not a planar graph. Multiple proofs of this impossibility are known, and form part of the proof of Kuratowski's theorem characterizing planar graphs by two forbidden subgraphs, one of which is $K_{3,3}$. The question of minimizing the number of crossings in drawings of complete bipartite graphs is known as Turán's brick factory problem, and for $K_{3,3}$ the minimum number of crossings is one. (Full article...)

Did you know

• ... that Ewa Ligocka cooked another mathematician's goose?
• ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
• ... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
• ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
• ... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
• ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
• ... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?

Did you know...

• ...an infinite, nonrepeating decimal can be represented using only the number 1 using continued fractions?
• ...that 253931039382791 and the following 18 prime numbers all end in the digit 1?
• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?
• … that the Riemann Hypothesis, one of the Millennium Problems, depends on the asymptotic growth of the Mertens Function?
• … that every positive integer can be written as the sum of three palindromic numbers in every number system with base 5 or greater?
• … that the best known lower bound for the length of the smallest superpermutation was first posted anonymously to the internet imageboard 4chan?

Featured pictures

• 
  Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals