Square

This article is about the shape. For other uses, see Square (disambiguation).

Square
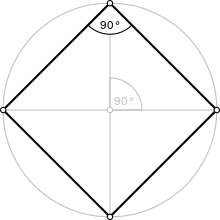A regular quadrilateral
Type	Regular polygon
Edges and vertices	4
Schläfli symbol	{4}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D4), order 2×4
Internal angle (degrees)	90°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal
Dual polygon	Self

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, with four equal angles, and of rhombuses, with four equal sides. As with rectangles, a square's angles are right angles (90 degrees, or π/2 radians).

Characterizations

A quadrilateral is a square if and only if it is any one of the following:

• A rectangle with four equal sides
• A rhombus with a right vertex angle
• A rhombus with all angles equal
• A parallelogram with one right vertex angle and two adjacent equal sides
• A quadrilateral with four equal sides and four right angles; that is, a quadrilateral that is both a rhombus and a rectangle
• A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals)
• A convex quadrilateral with successive sides $a$, $b$, $c$, $d$ whose area is $A={\tfrac {1}{2}}(a^{2}+c^{2})={\tfrac {1}{2}}(b^{2}+d^{2})$
• A parallelogram with equal diagonals that bisect the angles

Squares are the only regular polygons whose internal angle, central angle, and external angle are all equal (they are all right angles).

Properties

A square is a special case of a rhombus (equal sides, opposite equal angles), a kite (two pairs of adjacent equal sides), a trapezoid (one pair of opposite sides parallel), a parallelogram (all opposite sides parallel), a quadrilateral or tetragon (four-sided polygon), and a rectangle (opposite sides equal, right-angles), and therefore has all the properties of all these shapes, namely:

• All four internal angles of a square are equal (each being 360°/4 = 90°, a right angle).
• The central angle of a square is equal to 90° (360°/4).
• The external angle of a square is equal to 90°.
• The diagonals of a square are equal and bisect each other, meeting at 90°.
• The diagonal of a square bisects its internal angle, forming adjacent angles of 45°.
• All four sides of a square are equal.
• Opposite sides of a square are parallel.

A square has Schläfli symbol {4}. A truncated square, t{4}, is an octagon, {8}. An alternated square, h{4}, is a digon, {2}. The square is the two-dimensional case of two families of regular polytopes, the hypercubes and cross polytopes.

Perimeter and area

The area of a square is the product of the lengths of its sides.

The perimeter of a square whose four sides have length $\ell$ is

$P=4\ell$

and the area A is

$A=\ell ^{2}.$

Since four squared equals sixteen, a four by four square has an area equal to its perimeter. That is, it is an equable shape. The only other integer rectangle with such a property is a three by six rectangle.

In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.

The area can also be calculated using the diagonal d according to

$A={\frac {d^{2}}{2}}.$

In terms of the inradius r, the area of the square is

$A=4r^{2};$

hence the area of the inscribed circle is $\pi /4\approx 0.7854$ of that of the square.

Because it is a regular polygon, a square is the quadrilateral of least perimeter enclosing a given area. Dually, a square is the quadrilateral containing the largest area within a given perimeter. Indeed, if A and P are the area and perimeter enclosed by a quadrilateral, then the following isoperimetric inequality holds:

$16A\leq P^{2}$

with equality if and only if the quadrilateral is a square.

Other facts

• The diagonals of a square are ${\sqrt {2}}$ (about 1.414) times the length of a side of the square. This value, the square root of 2, was the first number proven to be irrational.
• A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).
• The square is a highly symmetric object. There are four lines of reflectional symmetry and it has rotational symmetry of order 4 (through 90°, 180° and 270°). Its symmetry group is the dihedral group D₄.
• If the inscribed circle of a square ABCD has tangency points E on AB, F on BC, G on CD, and H on DA, then for any point P on the inscribed circle,$$2(PH^{2}-PE^{2})=PD^{2}-PB^{2}.$$
• If $d_{i}$ is the distance from an arbitrary point in the plane to the i-th vertex of a square and $R$ is the circumradius of the square, then$${\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+3R^{4}=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+R^{2}\right)^{2}.$$
• If $L$ and $d_{i}$ are the distances from an arbitrary point in the plane to the centroid of the square and its four vertices respectively, then $$d_{1}^{2}+d_{3}^{2}=d_{2}^{2}+d_{4}^{2}=2(R^{2}+L^{2})$$ and $$d_{1}^{2}d_{3}^{2}+d_{2}^{2}d_{4}^{2}=2(R^{4}+L^{4}),$$ where $R$ is the circumradius of the square.

Coordinates and equations

$|x|+|y|=2$ plotted on Cartesian coordinates.

The coordinates for the vertices of a square with vertical and horizontal sides, centered at the origin and with side length 2 are (±1, ±1), while the interior of this square consists of all points (x_i, y_i) with −1 < x_i < 1 and −1 < y_i < 1. The equation

$\max(x^{2},y^{2})=1$

specifies the boundary of this square. This equation means "x² or y², whichever is larger, equals 1." The circumradius of this square (the radius of a circle drawn through the square's vertices) is half the square's diagonal, and is equal to ${\sqrt {2}}.$ Then the circumcircle has the equation

$x^{2}+y^{2}=2.$

Alternatively the equation

$\left|x-a\right|+\left|y-b\right|=r.$

can also be used to describe the boundary of a square with center coordinates (a, b), and a horizontal or vertical radius of r. The square is therefore the shape of a topological ball according to the L₁ distance metric.

Construction

The construction of a square with a given side, using a compass and straightedge, is given in Euclid's Elements. The existence of this construction means that squares are constructible polygons. A regular $n$-gon is constructible exactly when the odd prime factors of $n$ are distinct Fermat primes, and in the case of a square $n=4$ has no odd prime factors so this condition is vacuously true.

Square at a given circumcircle

Square at a given side length,
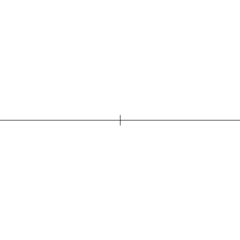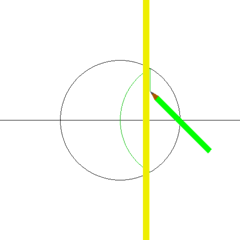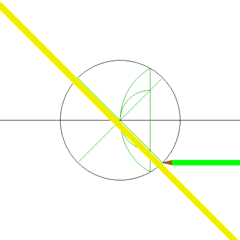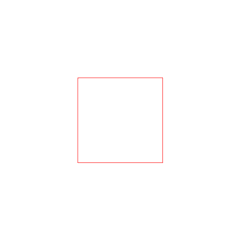
right angle by using Thales' theorem

Square at a given diagonal

Symmetry

Classification of quadrilaterals by their symmetry subgroups. The 8-fold symmetry of the square is labeled as r8, at the top of the image. The "gyrational square" below it corresponds to the subgroup of four orientation-preserving symmetries of a square, using rotations but not reflections.

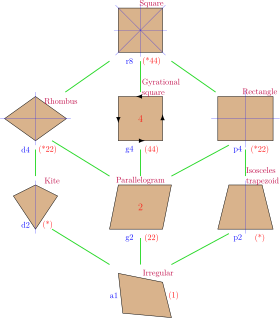
The square is the most symmetrical of the quadrilaterals. There are eight congruence transformations of the plane that take the square to itself:

• Leaving the square unchanged (the identity transformation)
• Rotation around the center of the square by 90°, 180°, or 270°
• Reflection across a diagonal, or across a centerline of the square, parallel to one of its sides.

Combining any two of these transformations by performing one after the other produces another symmetry. This operation on pairs of symmetries gives the eight symmetries of a square the mathematical structure of a point group, the dihedral group of order eight.

Inscribed squares

Main article: Inscribed square problem

A square is said to be inscribed in a curve whenever all four vertices of the square lie on the curve. It is an unsolved problem in mathematics, the inscribed square problem, whether every simple closed curve has an inscribed square. Some cases of this problem are known to be true; for instance, it is true for every smooth curve. For instance, a square can be inscribed on a circle, the circumscribed circle of the square, with circumradius $1/{\sqrt {2}}$ times the side length of the square. In terms of the circumradius $R$, the area of a square is $2R^{2}$, a fraction of $2/\pi \approx 64\%$ of the area of its circumscribed circle. As another special case of the inscribed square problem, a square can be inscribed on the boundary of any convex set. The only other regular polygon with this property is the equilateral triangle. More strongly, there exists a convex set on which no other regular polygon can be inscribed.

The Calabi triangle and the three placements of its largest square. The placement on the long side of the triangle is inscribed; the other two are not.

For an inscribed square in a triangle, at least one of the square's sides lies on a side of the triangle. Every acute triangle has three inscribed squares, one lying on each of its three sides. In a right triangle there are two inscribed squares, one touching the right angle of the triangle and the other lying on the opposite side. An obtuse triangle has only one inscribed square, with a side coinciding with part of the triangle's longest side.

An inscribed square can cover at most half the area of the triangle it is inscribed into. It is exactly half only when the square lies on a side of the triangle whose length equals the height of the triangle over that side. For a square that lies on a triangle side of length $x$, with height $h$, the square's side length will be $xh/(x+h)$. For any two inscribed squares in a triangle, the square that lies on the longer side of the triangle will have smaller area. In an acute triangle, the three inscribed squares have side lengths that are all within a factor of ${\tfrac {2}{3}}{\sqrt {2}}\approx 0.94$ of each other. The Calabi triangle, an obtuse triangle, shares with the equilateral triangle the property of having three different ways of placing the largest square that fits into it, but (because it is obtuse) only one of these three is inscribed.

Squaring the circle

A circle and square with the same area

Main article: Squaring the circle

Squaring the circle, proposed by ancient geometers, is the problem of constructing a square with the same area as a given circle, by using only a finite number of steps with compass and straightedge. In 1882, the task was proven to be impossible as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental number rather than an algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients.

Non-Euclidean geometry

Non-Euclidean geometry also has polygons with four equal sides and equal angles. These are often called squares, but some authors avoid calling them that, instead calling them regular quadrilaterals, because unlike Euclidean squares they cannot have right angles.

In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of Euclidean geometry, spherical squares have obtuse angles, larger than a right angle. Larger spherical squares have larger angles.

In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have acute angles, less than right angles. Larger hyperbolic squares have smaller angles.

Examples:

Two squares can tile the sphere with 2 squares around each vertex and 180-degree internal angles. Each square covers an entire hemisphere and their vertices lie along a great circle. This is an example of a dihedron. The Schläfli symbol is {4,2}.

Six squares can tile the sphere with 3 squares around each vertex and 120-degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}.

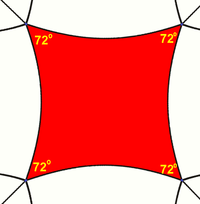Squares can tile the hyperbolic plane with 5 around each vertex, with each square having 72-degree internal angles. The Schläfli symbol is {4,5}. In fact, for any n ≥ 5 there is a hyperbolic tiling with n squares about each vertex.

See also

• Cube
• Pythagorean theorem
• Square lattice
• Square number
• Square root
• Squaring the square
• Squircle
• Unit square

External links

• Animated course (Construction, Circumference, Area)
• Definition and properties of a square With interactive applet
• Animated applet illustrating the area of a square